【例题讲解2】已知：平面直角坐标系中，四边形OABC的顶点分别为O（0，0）、A（5，0）、B（m，2）、C（m﹣5，2）．

（1）问：是否存在这样的m，使得在边BC上总存在点P，使∠OPA=90°？若存在，求出m的取值范围；若不存在，请说明理由．

（2）当∠AOC与∠OAB的平分线的交点Q在边BC上时，求m的值．

【简析】

（1）由四边形四个点的坐标易得OA=BC=5，BC∥OA，以OA为直径作⊙D，与直线BC分别交于点E、F，根据圆周角定理得∠OEA=∠OFA=90°，如图1，作DG⊥EF于G，连DE，则DE=OD=2.5，DG=2，根据垂径定理得EG=GF，接着利用勾股定理可计算出EG=1.5，于是得到E（1，2），F（4，2），即点P在E点和F

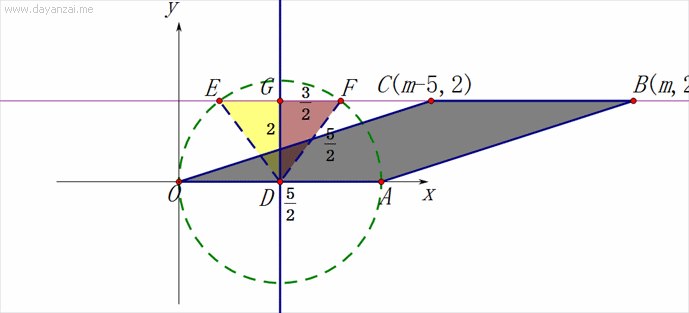
【小结】本题考查了的垂径定理并要会利用勾股定理计算线段的长，本题还考查了平行四边形的性质和等腰三角形的有关知识.